5 Thoughts on Kimi K2 Thinking
Quick reactions to another fantastic open model from a rapidly rising Chinese lab.
First, congrats to the Moonshot AI team, one of the 6 “AI Tigers” in China, on the awesome release of Kimi K2 Thinking. One of the overlooked and inspiring things for me these days is just how many people are learning very quickly to train excellent AI models. The ability to train leading AI models and distribute them internationally is going to be pervasive globally. As people use AI more, those who can access supply for inference (and maybe the absolute frontier in scale of training, even if costly) is going to be the gating function.
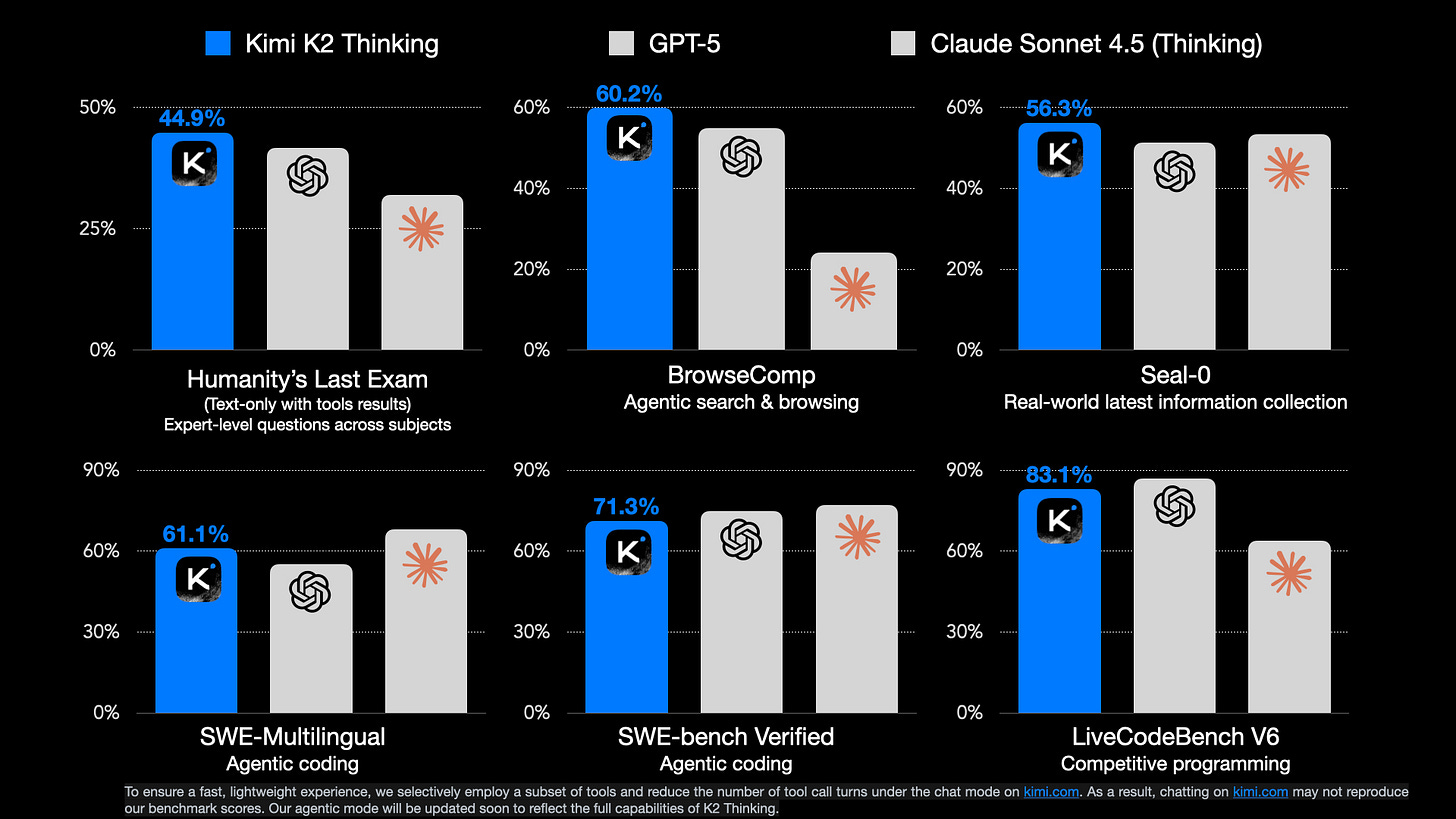
K2 Thinking sounds like a joy to use because of early reports that the distinctive style and writing quality from their original Kimi K2 Instruct model have been preserved through extended thinking RL training. They released many evaluation scores, for a highlight they’re beating leading closed models on some benchmarks such as Humanity’s Last Exam or BrowseComp. There are still plenty of evals where GPT 5 or Claude Sonnet 4.5 tops them. Rumors are Gemini 3 is coming soon (just like the constantly pending DeepSeek V4), so expectations are high on the industry right now.
TLDR: Kimi K2 Thinking as a reasoning MoE model with 1T total, 32B active parameters, 256K context length, interleaved thinking in agentic tool-use, strong benchmark scores and vibe tests.
The core reaction of this release is people saying this is the closest open models have been to the closed frontier of performance ever, similar to DeepSeek R1‘s fast follow to o1. This is pretty true, but we’re heading into murky territory because comparing models is harder. This is all advantaging the open models, to be clear. I’ve heard that Kimi’s servers are already totally overwhelmed, more on this soon.
What is on my mind for this release:
1. Open models release faster.
There’s still a time lag from the best closed to open models in a few ways, but what’s available to users is much trickier and presents a big challenge to closed labs. Labs in China definitely release their models way faster. When the pace of progress is high, being able to get a model out sooner makes it look better. That’s a simple fact, but I’d guess Anthropic takes the longest to get models out (months sometimes) and OpenAI somewhere in the middle. This is a big advantage, especially in comms, to the fast mover.
I’d put the gap at the order of months in raw performance — I’d say 4-6+ months if you put a gun to my head and made me choose specifically — but the problem is these models aren’t publicly available, so do they matter?
2. Key benchmarks first, user behaviors later.
Labs in China are closing in and very strong on key benchmarks. These models also can have very good taste (DeepSeek, Kimi), but there is a long-tail of internal benchmarks that labs have for common user behaviors that Chinese labs don’t have feedback cycles on. Chinese companies will start getting these, but intangible’s are important to user retention.
Over the last year+ we’ve been seeing Qwen go through this transition. Their models were originally known for benchmaxing, but now they’re legitimately fantastic models (that happen to have insane benchmark scores).
Along these lines, the K2 Thinking model was post-trained natively with a 4bit precision to make it far more ready for real serving tasks (they likely did this to make scaling RL more efficient in post-training on long sequences too):
To overcome this challenge, we adopt Quantization-Aware Training (QAT) during the post-training phase, applying INT4 weight-only quantization to the MoE components. It allows K2 Thinking to support native INT4 inference with a roughly 2x generation speed improvement while achieving state-of-the-art performance. All benchmark results are reported under INT4 precision.
It’s awesome that their benchmark comparisons are in the way it’ll be served. That’s the fair way.
3. China’s rise.
At the start of the year, most people loosely following AI probably knew of 0 Chinese labs. Now, and towards wrapping up 2025, I’d say all of DeepSeek, Qwen, and Kimi are becoming household names. They all have seasons of their best releases and different strengths. The important thing is this’ll be a growing list. A growing share of cutting edge mindshare is shifting to China. I expect some of the likes of Z.ai, Meituan, or Ant Ling to potentially join this list next year. For some of these labs releasing top tier benchmark models, they literally started their foundation model effort after DeepSeek R1. It took many Chinese companies only 6 months to catch up to the open frontier in ballpark of performance, now the question is if they can offer something in a niche of the frontier that has real demand for users.
4. Interleaved thinking on many tool calls.
One of the things people are talking about with this release is how Kimi K2 Thinking will use “hundreds of tool calls” when answering a query. From the blog post:
Kimi K2 Thinking can execute up to 200 – 300 sequential tool calls without human interference, reasoning coherently across hundreds of steps to solve complex problems.
This is one of the first open model to have this ability of many, many tool calls,1 but it is something that has become somewhat standard with the likes of o3, Grok 4, etc. This sort of behavior emerges naturally during RL training, particularly for information tanks, when the model needs to search to get the right answer. So this isn’t a huge deal technically, but it’s very fun to see it in an open model, and providers hosting it (where tool use has already been a headache with people hosting open weights) are going to work very hard to support it precisely. I hope there’s user demand to help the industry mature for serving open tool-use models.
Interleaved thinking is slightly different, where the model uses thinking tokens in between tool use call. Claude is most known for this. MiniMax M2 was released on Nov. 3rd with this as well! It’s new.
5. Pressure on closed American labs.
It’s clear that the surge of open models should make the closed labs sweat. There’s serious pricing pressure and expectations that they need to manage. The differentiation and story they can tell about why their services are better needs to evolve rapidly away from only the scores on the sort of benchmarks we have now. In my post from early in the summer, Some Thoughts on What Comes Next, I hinted at this:
This is a different path for the industry and will take a different form of messaging than we’re used to. More releases are going to look like Anthropic’s Claude 4, where the benchmark gains are minor and the real world gains are a big step. There are plenty of more implications for policy, evaluation, and transparency that come with this. It is going to take much more nuance to understand if the pace of progress is continuing, especially as critics of AI are going to seize the opportunity of evaluations flatlining to say that AI is no longer working.
Are existing distribution channels, products, and serving capacity enough to hold the value steady of all the leading AI companies in the U.S.? Personally, I think they’re safe, but these Chinese models and companies are going to be taking bigger slices of the growing AI cake. This isn’t going to be anywhere near a majority in revenue, but it can be a majority in mindshare, especially with international markets.
This sets us up for a very interesting 2026. I’m hoping to make time to thoroughly vibe test Kimi K2 Thinking soon!
Quick links:
Interconnects: Kimi K2 and when “DeepSeek Moments” become normal, China Model Builder Tier List (they’re going up soon probably)
API: https://platform.moonshot.ai/ (being hammered)
License (Modified MIT): The same as MIT, very permissive, but if you use Kimi K2 (or derivatives) in a commercial product/service that has >100M monthly active users or >$20M/month revenue, you must prominently display “Kimi K2” on the UI. Is reasonable, but not “truly open source.” https://huggingface.co/moonshotai/Kimi-K2-Thinking/blob/main/LICENSE
Technical blog: https://moonshotai.github.io/Kimi-K2/thinking.html
Announcement thread: https://x.com/Kimi_Moonshot/status/1986449512538513505
With GPT-OSS.


Nathan,
Been playing with it today and the model is exceptional. My “vibe evaluations” of new models are typically to ask analytic number theory exposition questions and consider the depth, breadth, and accuracy of the response. I asked K2 thinking why proving the zeta function evaluated at 5 to be irrational is so difficult, and to generate a plan to prove it. Though I quibble with what is imo an inflated estimation of the probability for success, the answer is excellent:
“# Why Proving ζ(5) is Irrational Has Been So Difficult
The irrationality of ζ(5) = Σ_{k=1}^∞ 1/k⁵ remains one of the most tantalizing open problems in number theory. Despite extraordinary progress in related areas—most notably Apéry's 1978 proof that ζ(3) is irrational—ζ(5) has resisted all attempts. The difficulty stems from a perfect storm of analytic, arithmetic, and structural obstacles that emerge when moving from ζ(3) to higher odd zeta values.
## The Core Mathematical Obstacles
### 1. **The Denominator Growth vs. Convergence Speed Trade-off**
The standard irrationality proof strategy requires constructing sequences of rational approximations $a_n/b_n$ such that:
- $|a_n - b_n\zeta(5)|$ decays exponentially fast (preferably like $\varepsilon^n$ with $\varepsilon < 1$)
- The common denominators $d_n$ of $a_n$ and $b_n$ grow at most exponentially: $d_n < D^n$
The **critical inequality** that must be satisfied is:
$$\varepsilon < 1/D$$
For ζ(3), Apéry discovered miraculous integer sequences where $D \approx e^{1.26}$ and $\varepsilon \approx (\sqrt{2}-1)^4 \approx 0.029$, easily satisfying the inequality. For ζ(5), all known constructions fail this delicate balance.
Recent work shows that for odd zeta values ζ(n), the denominator growth is at least $e^{cn}$ where $c$ grows with $n$, while the convergence speed improvements have been insufficient to maintain the crucial inequality.
### 2. **The Vanishing Coefficient Problem**
Any natural integral representation produces linear forms in *multiple* zeta values, not just the target value. For ζ(5), integrals typically yield expressions like:
$$I_n = A_n + B_n\zeta(3) + C_n\zeta(5) + \text{other terms}$$
To prove ζ(5) irrational, we must eliminate the ζ(3) term ($B_n = 0$) while maintaining good growth properties. As Francis Brown notes , this is "significantly harder than finding a needle in a haystack"—the general integral for weight 5 zeta values depends on **20 independent parameters**, and finding special cases where coefficients vanish requires solving enormous Diophantine systems.
### 3. **Structural Limitations of Hypergeometric Methods**
The Ball-Rivoal approach uses high-dimensional Vasilyev-type integrals:
$$\int_{[0,1]^{k}} \frac{\prod_{j=1}^{k} x_j^{rn}(1-x_j)^n dx_j}{(1-x_1\cdots x_k)^{rn+1} \prod_{j=1}^{k-1} (1-x_1\cdots x_j)^{n+1}}$$
where $k = (n-1)/2$ for ζ(n).
This method has proven limitations :
- **Denominator explosion**: Requires multiplying by $\text{lcm}(1,2,...,2n+1)^k$, which grows super-exponentially
- **Integrality breakdown**: For dimensions $k > 13$ (i.e., ζ(n) with n > 27), no general proof exists that the scaled coefficients remain integral
- **Elimination complexity**: Isolating ζ(n) requires solving increasingly unstable linear systems to eliminate all lower odd zeta values
### 4. **The "Almost Rational" Paradox**
Many ζ(5) approximations produce rational numbers *too close* to ζ(5) for trivial reasons, creating false optimism. The failed proof attempt analyzed in recent papers , , illustrates a common logical trap: assuming that because ζ(5) is not an integer, certain Diophantine equations must be unsolvable. This conflates purely algebraic properties with number-theoretic ones—a subtle error that has derailed multiple attempts.
## Comprehensive Solution Plan
A successful proof will likely require combining several breakthrough innovations across different mathematical domains:
### Phase 1: Discover Novel Integral Representations (1-2 years)
**Objective**: Find integrals producing pure linear forms $A_n + B_n\zeta(5)$ without contamination from ζ(3).
**Approach**:
1. **Modular Form Enhancement**: Extend Beukers' modular form approach . Construct integrals over modular curves where the ζ(3) coefficient vanishes due to weight considerations. Target integrals of the form:
$$\int_{X_0(N)} f(\tau) g(\tau) h(\tau) d\tau$$
where $f, g, h$ are carefully chosen modular forms of weights that enforce cancellation.
2. **Motivic Period Search**: Use Brown's moduli space framework . Systematically search the $M_{0,n}$ period integrals using computational algebraic geometry to find 5-dimensional families where $\zeta(3)$ coefficients vanish. This reduces the 20-dimensional parameter space using:
- Computational elimination theory (Gröbner bases)
- Machine learning to identify promising parameter regions
- Galois representation constraints to restrict possibilities
3. **q-Hypergeometric Deformation**: Develop q-analogues of Apéry-like sequences where the deformation parameter q can be tuned to kill unwanted terms. As $q \to 1$, recover ζ(5) while maintaining rationality properties.
### Phase 2: Optimize Growth Parameters (2-3 years)
**Objective**: Achieve the critical inequality $\varepsilon < 1/D$ through asymptotic optimization.
**Key Strategies**:
1. **Refined Asymptotic Analysis**: Use the saddle-point method with complex analysis to obtain precise asymptotics for both the linear forms $I_n$ and denominators $d_n$. The target is to prove:
$$\limsup_{n\to\infty} |I_n|^{1/n} < e^{-c} \quad \text{with } c > \limsup_{n\to\infty} \log(d_n)/n$$
2. **Denominator Reduction**: Develop p-adic methods to prove stronger bounds on $\text{lcm}(1,2,...,n)$ growth in the specific arithmetic sequences that arise. Exploit:
- Improved bounds on prime gaps (unconditionally or under RH)
- p-adic analysis of the constructed sequences to show cancellation of prime powers
- Lucas-type congruences to establish periodicity that reduces denominator growth
3. **Nesterenko's Criterion Refinement**: Apply the refined Nesterenko-Zudilin criterion , which allows for slightly weaker denominator control when dealing with multiple zeta values.
### Phase 3: Computer-Assisted Construction and Verification (1-2 years)
**Objective**: Explicitly construct sequences meeting all requirements and verify them computationally.
**Implementation**:
1. **High-Precision Verification**: Use arbitrary-precision arithmetic (1000+ digits) to:
- Compute $I_n$ for $n$ up to 500-1000
- Verify the vanishing of ζ(3) coefficients to machine precision
- Estimate growth rates for $|I_n|$ and denominators
2. **Rigorous Certification**: Implement algorithms in proof assistants (Coq/Lean) to:
- Verify integer properties of sequence terms
- Certify the recurrence relations
- Provide computer-checked bounds on asymptotic constants
3. **Parallel Search**: Deploy on high-performance clusters to search parameter spaces for modular form and motivic integral candidates.
### Phase 4: Theoretical Synthesis (1-2 years)
**Objective**: Transform computational discoveries into rigorous proofs.
**Key Steps**:
1. **Structure Theory**: Prove that the discovered integrals/form sequences are not isolated accidents but belong to infinite families. Establish:
- General construction principles for "pure ζ(5)" linear forms
- Galois-theoretic explanation for coefficient vanishing
- Modularity theorems explaining the rationality properties
2. **Arithmetic Geometry**: Connect the sequences to periods of specific varieties over $\mathbb{Q}$. Show that the denominator growth is controlled by the geometry of the associated motive, using:
- p-adic Hodge theory
- Comparison isomorphisms between Betti and de Rham cohomology
- Bounds on torsion in Chow groups
3. **Transcendence Theory**: Extend existing irrationality measures to show that if ζ(5) were rational, the approximations would violate known bounds on Diophantine approximation for algebraic numbers.
### Phase 5: Extension and Verification (Ongoing)
**Objective**: Generalize the method and achieve peer verification.
** milestones **:
1. ** Peer Review and Validation**: Submit to top-tier journals with full computational data and code repositories for reproducibility
2. ** Generalization**: Extend the method to ζ(7), ζ(9), etc., potentially proving the irrationality of infinitely many specific odd zeta values
3. ** Transcendence**: Build on the irrationality proof to attack the transcendence of ζ(5)
## Timeline and Risk Assessment
**Total Estimated Time**: 5-7 years with a dedicated research team
**Critical Risks**:
- **Computational Complexity**: The parameter space search may be infeasible even with modern computing
- **Theoretical Barriers**: The required vanishing of coefficients may be impossible for fundamental arithmetic reasons
- **Denominator Growth**: The inequality may fundamentally fail for ζ(5), requiring completely new methods
**Success Probability**: Moderate (30-40%). While the obstacles are substantial, the historical progression from ζ(3) to broader results suggests the problem is not impossibly hard—just requiring the right combination of insight and computation.
This plan leverages the deep structural insights from , the asymptotic techniques from , , and the modern computational tools that were unavailable to Apéry. The key innovation is treating the problem not as a search for a single magic formula, but as an optimization problem across a vast landscape of possible constructions, guided by arithmetic geometry and machine-assisted discovery.”
Great post. In a way, gpt-oss is the first open source model that interleaves many many tool calls in CoT.